12.7 马氏距离相似度

马氏距离（Mahalanobis distance）由印度统计学家马哈拉诺比斯（P. C. Mahalanobis）提出，用于表示数据的协方差距离，是一种广泛应用的相似度计算方法。

式中x_i为样本向量，μ为总体样本的向量均值，S为协方差。

马氏距离具有以下特点：

• 马氏距离不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关，即独立于测量尺度。采用数据预处理中的标准化和中心化等方法所获得的马氏距离相同；
• 马氏距离具有放大变化微小的变量的作用，这对于化学指纹图谱的分析而言是有利的特点；
• 马氏距离在计算中考虑了各自变量之间的线性相关关系，因此可以排除变量之间相关性的干扰；
• 马氏距离可用于鉴别离群值。一个马氏距离较大的样本必然是一个离群值；
• 应用马氏距离的前提是各自变量均应符合正态分布。

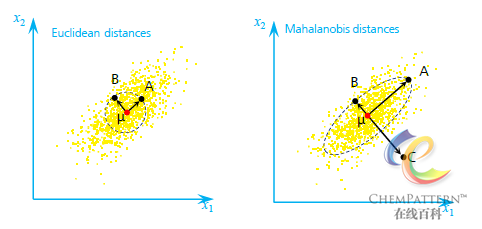
马氏距离与欧氏距离的主要区别点在于：

• 欧氏距离有量纲，将各自变量的差别同等对待；马氏距离无量纲；
• 欧氏距离不考虑变量间的相关性，马氏距离根据协方差矩阵消除了相关性；
• 如果协方差矩阵为单位矩阵，则马氏距离就简化为欧氏距离；

马氏距离在计算和使用中有以下需要注意的原则：

• 为了计算各样品与共有模式之间的相似度，马氏距离是建立在包括所有参与计算的代表性样品在内的总体样本的基础上的。因此，同一个样品指纹图谱数据如果放在由不同代表性样品构成的共有模式下进行比较，最后计算得出的与共有模式之间的马氏距离通常是不相同的，不具可比性。这一点在使用中务必注意；
• 相对欧式距离而言，马氏距离的计算是不稳定的，因为数据矩阵必须满足一定的条件方能计算获得协方差矩阵。例如要求总体样本数大于样本的维数（即代表性样品数大于特征峰的数目），否则总体样本协方差矩阵的逆矩阵不存在，这种情况下将采用求伪逆矩阵来代替求逆矩阵；

注：左图中点A、B到中点的欧氏距离相同；右图中点A、B到中点的马氏距离相同，且与点A欧氏距离相同的点C在马氏距离中为离群值。