12.9 原始数据矩阵

用于化学计量学分析的原始数据的二维矩阵形式X_{m x n}通常可由m个待分析样本（或称观测）的n个自变量（根据上下文亦可称指标、特征值、共有峰等）来描述。此外还涉及用于回归模型的因变量（亦作应变量）矩阵，以及用于模式识别的分类信息矩阵等。

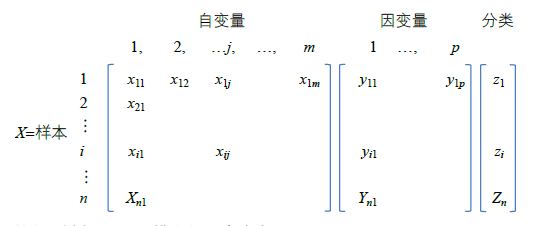
其中，样本i可以用模式向量{\vec x_i}来表示：

上述矩阵也可以用如下的简图形式来表示：

化学计量学及化学指纹图谱分析中的自变量具有以下特点：

• 不同化学分析仪器类型的解决方案都有固定的自变量类型如成分含量、光谱吸收值等等，在ChemPattern中自变量的数量通常由解决方案所建立的共有模式决定；
• 自变量的测量尺度（方法）和计量单位都是一致的；
• 不同自变量的测量值变化幅度可能差异很大，需要有针对性的数据预处理；
• 自变量个数通常较多（可能多于样本数），对于开展一些分析方法会有限制，需要有针对性的数据预处理，如数据降维。

通过设定样本因变量，可建立该类样本的数学回归模型，从而发现并解释样品因变量（表观性质）与自变量（内在特征）之间的联系，并对未知样品的属性进行预测。因变量具有以下特点：

• 与自变量不同，因变量的类型没有限定。任何用于定性、定量的指标均可作为样本的因变量从而进行回归建模分析，可采用的因变量类型如下：
• 标称标度（定性），亦称计数数据，例如：真伪（+1, -1），有无（1, 0）等；
• 顺序标度（定性），亦称等级数据，例如：微苦、较苦、很苦（1, 2, 3）；治愈、显效、好转、无效（1-4）等；
• 算术标度（定量），亦称计量数据，例如：总茶多酚含量（0.8, 1.1, 6.2）等。又可细分为连续型和离散型；
• 因变量的测量尺度（方法）和计量单位可能很不同，需要有针对性的数据预处理。