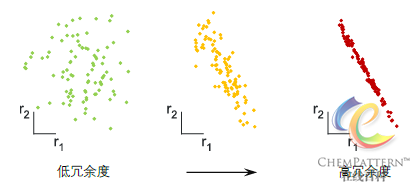
右图:两个测量值之间具有高度的线性相关,因此两次测量是高度冗余的,冗余度≈2。
主成分分析(Principal component analysis,PCA)由英国统计学家卡尔•皮尔逊于1901年提出。PCA是最经典和应用最广泛的以特征向量分析为基础的多元统计方法,在不同的应用领域中,又被称为奇异值分解、特征值分解、谱分解、Hotelling变换和离散Karhunen-Loeve变换等。
主成分分析通过正交相似性变换,将一组符合多元正态分布的具有多重共线性(图12-15)的变量转换为被称为主成分(PCs)的一组线性非相关的新变量的线性组合,从而起到揭示数据内部结构,以及简化数据维数的投影作用。

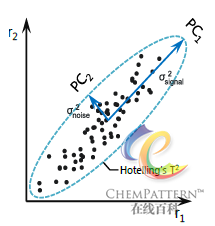
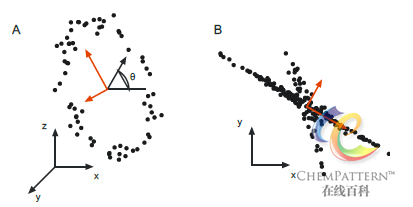
主成分分析在原始空间中顺序找出一组相互正交的坐标轴(主成分),其中第一个主成分总是体现了数据集中的最大方差,接下来的每个主成分依次具有与之前主成分正交的最大方差(图12-16)。通常所获得的前几个主成分即贡献了绝大部分的方差,因此最终需要保留的主成分个数一般远小于原始变量的个数。
上式为主成分分析的矩阵形式,样品数据矩阵X(n×m)分解为得分(Score)矩阵T和载荷(Loading)矩阵P。每个得分向量t即为样品X在其对应载荷向量p方向上的投影, ti称为原始自变量X1,X2,…, Xm的第i个主成分:
{t_i} = X{p_i} = {X_1}{p_{i1}} + {X_2}{p_{i2}} + \cdots + {X_m}{p_{im}},i = 1,2, \cdots m以m个指标Xm的线性组合方式可表示为:
\begin{gathered} {T_1} = {\alpha _{11}}{X_1} + {\alpha _{12}}{X_2} + \cdots + {\alpha _{1m}}{X_m} \hfill \\ {T_2} = {\alpha _{21}}{X_1} + {\alpha _{22}}{X_2} + \cdots + {\alpha _{2m}}{X_m} \hfill \\ {\text{ }} \vdots \hfill \\ {T_m} = {\alpha _{m1}}{X_1} + {\alpha _{m2}}{X_2} + \cdots + {\alpha _{mm}}{X_m} \hfill \\ \end{gathered}主成分分析的求解通常由特征值分解或奇异值分解实现。
该方法对X的协方差矩阵XTX或相关矩阵R的特征值-特征向量问题进行求解,其中u和λ分别称为特征向量(eigenvector)和特征值(eigenvalue)。
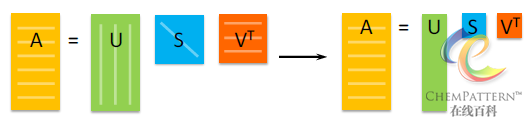
奇异值分解与主成分分析是完全等效的。上式中,U为标准列正交(列特征向量)矩阵,VT为标准行正交(行特征向量)矩阵, S为矩阵X的奇异值的对角矩阵,且S等于协方差矩阵XTX的特征值λ的平方根。US即为得分矩阵T,而V即是载荷矩阵P。奇异值分解的矩阵形式示意图见图12-17。
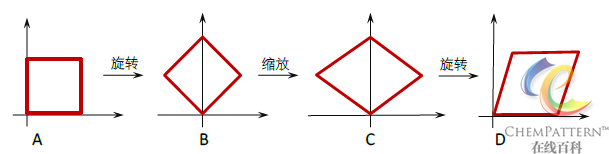
矩阵奇异值分解的几何意义实质是将对原始矩阵的任何变换看作两个正交旋转(U和VT)和一个缩放变换(S)的复合,如图12-18所示:
奇异值分解是主成分分析更为现代的实现方法。其直接对数据矩阵进行求解,因此计算结果与特征值分解方法存在差异。如果希望在ChemPattern中重现特征分值解的结果,可在计算主成分分析时选择“针对变量的标度化”数据预处理方法。
如何选取恰当的主成分个数,使其可以最大程度地解释原数据的信息,并同时尽量去除噪音等的影响,是进行主成分分析时需要考虑的重要问题。以下为其中部分方法:
其中,ln|R|为相关系数矩阵行列式的自然对数,(p2-p)为卡方检验的自由度,p为自变量数,n为样本数。做假设H0=数据的协方差矩阵为单位矩阵,即数据在向量空间中呈球形分布的检验。然而,卡方检验受样本数的影响较大,因此该有效性检验较为宽松,在使用中应结合具体情况加以判别。
式中m为样本数,n为主成分数,F代表显著性为α的F检验。在得分图上超出T2置信区间椭圆边界的数据点,代表该样本在当前PCA模型的对应主成分轴上中未得到较好的投影,属于当前PCA模型不能恰当解释的相对特殊的离群值。