谱系图(Dendrogram)最早起源于由瑞典博物学家卡尔•林奈创建并发展的传统生物分类学。在经典的系统聚类分析(Hierarchical clustering analysis, HCA)中,单个的生物样本和与其具有最相似特征属性的样本优先结合为簇(Cluster)这一基本单位,从而渐次聚合构成了种、属、科、目等更高分类级别,与之类似的还有系统进化/种系发生树(Phylogenetic tree,图12-22)。系统聚类方法作为诸多领域的通用方法,目前已在分析化学与化学计量学中得到了广泛应用。
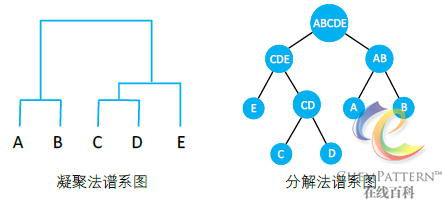
谱系聚类发展至今已形成了诸多方法,与之对应的还有非谱系聚类法(如k-均值聚类)。前者最常见的方法如图12-23所示,ChemPattern中所提供的为凝聚法系统聚类分析,以及其扩展形式双向聚类分析(亦称聚类分析热图)。
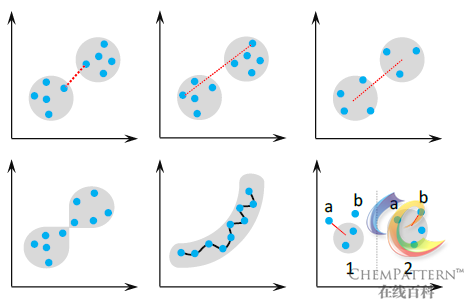
进行系统聚类分析需要首先指定样本间距离的测度类型,以及连接方法。常用的距离计算方法一般有欧氏距离、街区距离、马氏距离,以及相关系数和夹角余弦相似度等。
基于距离测度的各类系统聚类的连接方法都可由以下通式表示,其对应参数取值如下表所示,其中s代表距离矩阵,r、(p+q)分别代表两个待结合的簇:
s\left( {r,p + q} \right) = {\alpha _p}s\left( {r,p} \right) + {\alpha _q}s\left( {r,q} \right) + {\beta _p}s\left( {p,q} \right) + \gamma \left| {s\left( {r,p} \right) - s\left( {r,q} \right)} \right|| 连接方法 | αp | αq | β | γ | s(r, p+q) |
|---|---|---|---|---|---|
| 近邻法 (最短距离法) |
½ | ½ | 0 | ½ | \dpi{100}\min \left( {s\left( {r,p} \right),s\left( {r,q} \right)} \right) |
| 远邻法 (最长距离法) |
½ | ½ | 0 | ½ | \dpi{100}\max \left( {s\left( {r,p} \right),s\left( {r,q} \right)} \right) |
| 加权平均距离法 | ½ | ½ | 0 | 0 | \dpi{100}\frac{{s\left( {r,p} \right),s\left( {r,q} \right)}}{2} |
| 未加权平均距离法 | \dpi{100}\frac{{{m_p}}}{{{m_p} + {m_q}}} | \dpi{100}\frac{{{m_q}}}{{{m_p} + {m_q}}} | 0 | 0 | \dpi{100}\frac{{{m_p}s\left( {r,p} \right) + {m_q}s\left( {r,q} \right)}}{{{m_p} + {m_q}}} |
| 加权重心法 (中间距离法) |
½ | ½ | -¼ | 0 | \dpi{100}\frac{{s\left( {r,p} \right) + s\left( {r,q} \right)}}{2} - \frac{{s\left( {p,q} \right)}}{4} |
| 未加权重心法 | \dpi{100}\frac{{{m_p}}}{{{m_p} + {m_q}}} | \dpi{100}\frac{{{m_q}}}{{{m_p} + {m_q}}} | \dpi{100}\frac{{ - {m_p}{m_q}}}{{{{\left( {{m_p} + {m_q}} \right)}^2}}} | 0 | \dpi{100}\frac{{{m_p}s\left( {r,p} \right) + {m_q}s\left( {r,q} \right)}}{{{m_p} + {m_q}}} - \frac{{{m_p}{m_q}}}{{{{\left( {{m_p} + {m_q}} \right)}^2}}}s\left( {p,q} \right) |
| 误差平方和法 (沃德法) |
\dpi{100}\frac{{{m_p} + {m_r}}}{{{m_p} + {m_q} + {m_r}}} | \dpi{100}\frac{{{m_q} + {m_r}}}{{{m_p} + {m_q} + {m_r}}} | \dpi{100}\frac{{ - {m_r}}}{{{m_p} + {m_q} + {m_r}}} | 0 | \dpi{100}\frac{{\left( {{m_r} + {m_p}} \right)s\left( {r,p} \right) + \left( {{m_r} + {m_q}} \right)s\left( {r,q} \right) - {m_r}s\left( {p,q} \right)}}{{{m_p} + {m_q} + {m_r}}} |
谱系图的不同连接方法在使用中各有利弊(图12-24),需要结合应用中的具体情况进行判断。但一般来说,平均距离法和误差平方和法的聚类效果通常相对占优。