12.22 自组织映射人工神经网络

自组织映射人工神经网络（self-organizing map，SOM，亦称Kohonen network）由芬兰数学家Teuvo Kohonen于1981年提出。SOM是一种无监督的人工神经网络，利用竞争原则来进行网络的学习，并将高维数据非线性地映射到低维空间中。这种投影通过近邻函数保持了输入空间的拓扑关系，因此通过训练，未知的相似样本输入将被投影到网格上相同或邻近的神经元或称节点（node）上。

拓扑结构

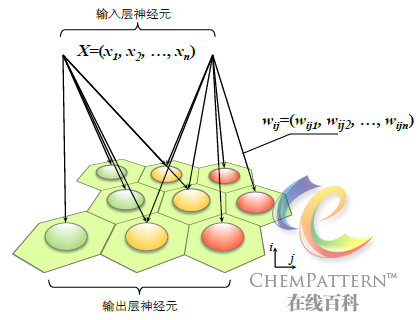
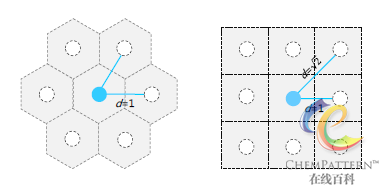
SOM的双层网络结构如图12-30所示，它由输入层（输入节点及权值）和输出层（竞争层）构成。其中输入层具有和输入空间相同的维数。输出层通常由神经元组成的二维平面网格（阵列）构成，每个神经元和一个权值向量相联系，权值向量具有和输入层相同的维数。神经元之间的连接方式采用正方形或六边形拓扑结构（图12-31）。

左图为神经元网格的六边形拓扑结构，其中每个神经元与其相邻神经元之间的间距都为单位距离；右图为神经元网格的正方形拓扑结构，其中每个神经元与其相邻神经元存在两种间距。

工作原理

SOM的目标是对于特定的输入模式使得网络中的不同部分按照相关性程度进行反馈，这种工作机制在很大程度上来自对大脑皮质功能区如何处理视觉、听觉等感官信息的仿生学模拟，其核心实现架构包括两个重要方面：竞争性神经网络以及神经元突触的可塑性学习。

SOM是人工神经网络以及多元统计方法中不可多得的可视化分析方法之一，任意维数的原始数据都可以在保持拓扑结构不变的情况下映射到二维空间内，因此广泛适用于复杂体系数据的可视化、降维、模式识别以及数据挖掘。

自组织映射网络训练的示意。蓝色区域代表训练集样本的分布，白色符号为当前待训练样本。起初（左图）网格中的神经元为线性（或随机）权值初始化，其中最接近样本的一个神经元（黄色所示）向样本方向移动，并带动邻近神经元也产生了不同程度的位移。经过多次递归后（右图），网格即完成了对样本分布的拓扑结构近似。wikipedia.org

SOM的基本算法可大致概括如下：

• 随机初始化各神经元权重向量；
• 读取一个样本的输入向量D(t)；
• 计算输入向量和网络中每个神经元权重向量间的欧氏距离相似度；
• 检索相似度最大的神经元，将其作为最佳匹配单元（Best matching unit, BMU）；
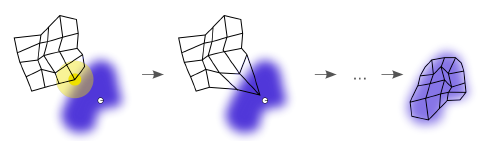
• 更新包括BMU在内的邻近神经元，使它们向输入向量靠近（图12-32）：
{W_v}(s + 1) = {W_v}(s) + \Theta (u,v,s) \times \alpha (s) \times (D(t) - {W_v}(s))

其中，WV为当前神经元v的权重，s为当前递归值，\Theta (u,v,s)为距离约束值，亦称近邻函数（图12-33），通常采用高斯函数；u为BMU，\alpha (s)为学习约束值。在最初的递归过程中，权重的调整（即神经元的兴奋或抑制）这一自组织过程可以是作用于网络全局，当受激励神经元个数随近邻函数的衰减减少到只有数个时，权重逐步收敛于局部估计量。

• 重复以上第2步起的过程，直至达到训练结束条件为止。

以一个训练完毕的由3个自变量所组成的输入向量构成的自组织映射网络为例，显示了神经元对于输入模式的记忆。左图为各神经元权重中3个自变量所占比例饼图，右图为3个自变量的数据折线图，显示了相似模式的样本一定都分布在彼此邻近的神经元中。

特点概述

与其它人工神经网络以及多变量分析方法相比，SOM具有以下显著特点：

• SOM的聚类结果是非线性的，因此即使是超平面不可分的数据，仍可通过与k-近邻法（12.23）联用从而获得正确的分类预测和模式识别结果。
• SOM天然地可以处理任意维度样本数据（非指自变量维度）的输入，因此并不局限于示例中的n×1输入向量，也可以是n×m、n×m×p等构造。此外，SOM可以映射到任意低维的空间，由于观察方便，二维映射空间是其中最常用的。
• SOM也被称为非线性的泛化PCA技术，其性能通常优于主成分分析。这也说明比主成分分析更复杂的矩阵分解可在以神经元为单位的大规模并行计算架构上，通过简单的数学运算以一种自然的方式获得实现。
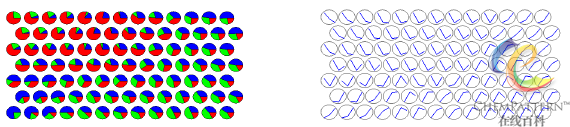
• SOM的训练过程高效并且稳健，训练集残差通常会快速下降并最终总是收敛得到全局而非局部的最优解（图12-35）。并且当递归训练次数达到足够大时，样本的BMU神经元总是倾向于在投影平面上均匀分布。
• 同其他人工神经网络方法一样，SOM的优异性能主要来自于特殊的结构工程设计，而非发端于严格的数学推理，用后者完全解释神经网络仍比较困难，目前只有一维SOM的数学原理获得了完整阐述。

从左至右，从上至下：采用经典的Fisher's Iris数据对SOM神经网络进行训练为例，图1为SOM神经网络的无监督学习结果，显示3个鸢尾属植物品种都获得了清晰区分；图2为4个自变量中的花瓣长度值的权重分布，显示其与样本分布一致，并且对分类影响较显著；图3-4为SOM U矩阵（记录每个神经元之间空间距离的矩阵），其中图4叠加样本分布散点图。从图中可观察到山鸢尾（Iris setosa）与其它种区别明显，而变色鸢尾（I. versicolor）与维吉尼亚鸢尾（I. virginica）的区别相对不很显著，但其在SOM的拓扑投影中仍可得到正确的区分，说明二者存在系统差异。

以前一个例子的神经网络训练为例（近邻半径系数0.96，学习速度系数0.99，初始学习速度1.0），从上方的聚类图中可观察到网络收敛速度较快，此外起初相似样本的BMU神经元之间的凝聚效应强烈，不同类别样本的距离较远。而当递归训练次数足够大时，样本的BMU神经元在投影平面形成均匀分布。从下方的U距离矩阵中可观察到整个映射图的收敛过程。

模型质量评价

对SOM模型质量的评价主要从模型残差、预测能力以及模型拓扑质量等几方面进行：

• 模型残差e = \sum\limits_{i = 1}^m {{{({X_i} - {W_{BMUi}})}^2}} /\sum\limits_{i = 1}^m {X_i^2}；
• 拓扑拟合质量 = 每个训练集中样本的最优拟合单元BMU与次优拟合单元（SMU）神经元相邻的情况占总样本数的百分比；
• BMU重叠率 = 投影于同一个BMU神经元的不同样本所占总样本数的百分比；
• BMU错误分类率 = 投影于同一个BMU神经元的所属分类不同的样本所占总样本数的百分比。

模型残差体现了模型对训练集的拟合程度，是评价训练质量的主要参数。但该值并非越低越好，在使用中需要对网络过度训练可能导致的模型泛化能力下降的问题引起足够的重视，并将递归训练次数作为模型优化时考察的参数之一。

神经元数目

对于网络神经元（网格）数目的选择及优化，有以下原则可供参考：

• 由于网络自身的构造特点，为了更好地拟合输入向量的空间分布，网格高宽比应尽量呈矩形而非正方形。更进一步地，可按照原始数据在其主要维度中的分布范围（如主成分分析中前两个主成分的特征值的比值）进行设定；
• 模型中所需的神经元数量通常可视情况而定，与训练集样本数无必然关联。所选择的SOM模型只需保证较低的BMU错误分类率和模式识别错误率即说明建模是成功的。但模型残差并非越小越好，否则有可能导致网络的过拟合。
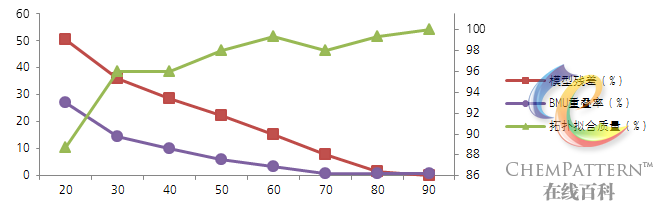
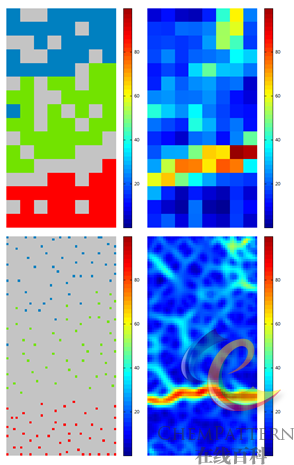
• 通常网格尺寸越大则模型质量及分辨率越好（图12-36），模式识别时的BMU冗余度也较大，但缺点是计算量呈网格边长的近指数倍增长，因此使用中需要在网络质量和网格尺寸（训练耗时）之间寻求平衡点。
• SOM网络的学习和自适应能力较强，因此上述规则仅作一般性参考。

常见事项

最后是对SOM网络在应用过程中一些常见事项的建议：

• 由于网络自身的构造特点，特别是在模式识别时，建议对所输入数据应进行必要的数据预处理；
• 由于初始时为随机权值向量，因此对于同样的训练集，每次重新训练后所获得的SOM模型可能有所不同，体现在映射平面的坐标可能发生90o旋转（正方形网格尺寸）或呈镜像（矩形网格尺寸），这种情况并不影响对结果的分析；
• SOM网络的可调参数较多，且重新建模较耗时，因此在模式识别的交叉验证过程中，不支持对SOM的可调参数进行评价。如果需要比较某一参数的不同取值对网络模型性能的影响，则依次进行交叉验证即可。