ChemPattern百科 - 化学计量学白皮书

12.24 支持向量机

支持向量机（support vector machine，SVM）是一种有监督的机器学习方法，属于一般化线性分类器。支持向量机作为统计学习理论（SLT，Statistical Learning Theory）的集大成者，在20世纪90年代初由当时美国AT&T贝尔实验室的Vladimir N. Vapnik等人提出。该方法在小样本、非线性和高维数据空间的模式识别问题上拥有传统模式识别方法所不具备的独特优势，因此目前在涉及统计分类以及回归分析的诸多相关领域中得到了广泛的应用，特别适用于复杂体系分析及数据挖掘。

支持向量机的基本原理是将样本的低维向量非线性地隐式映射到高维特征空间，并在分开两类分类之间的超平面两侧建立一对互相平行的支持超平面并使其之间的距离（几何边缘，geometrical margin）最大化。在其方法命名中，支持向量是指从两个分类的样本训练集中筛选得到的一组样本子集，使得对特征空间中样本子集的划分等价于对整个训练集的划分。这组用于定义（支撑）将两类类别划分开来的超平面上的向量即称为支持向量。支持向量机即指以支持向量为核心原理的机器学习分类器。

从Vapnik在1963年首次提出支持向量概念直至最终发展为支持向量机，其理论体系和实现方法分别主要来自以下三个不同研究领域的进展：

支持向量机理论。包括最大间隔分类超平面、松弛变量与软间隔优化，置信风险定量评价等；
核空间与核函数理论。包括非线性映射、高维特征空间、隐式映射等；
最优化理论。包括二次规划，对偶问题，SMO算法等。

上述理论中的主要实现方法将结合以下具体算法进行介绍。

支持向量机算法实现

1）线性分类器

假定两类线性可分的训练集数据为：

({x_1},{y_1}),...,({x_n},{y_n}),x \in {\mathbb{R}^n},y \in \{ + 1, - 1\}

其中样本数为n，特征自变量数为d，y为类别标号。则d维空间中的线性判别函数及其分类超平面方程为：

\begin{gathered} f(x) = {w^T}x + b \hfill \\ {w^T}x + b = 0,w \in {\mathbb{R}^d},b \in \mathbb{R} \hfill \\ \end{gathered}

2）广义最优分类面（超平面）

将判别函数通过引入缩放因子\left\| w \right\|进行归一化，使两类样本都满足\left| {f(x)} \right| \geqslant 1 ，则此时离分类面最近的样本的\left| {f(x)} \right| = 1，因此分类的几何间隔等于2/\left\| w \right\|。所以使分类间隔最大等价于使\left\| w \right\|最小。同时为了保证分类超平面能够对样本进行正确分类，还要求满足：

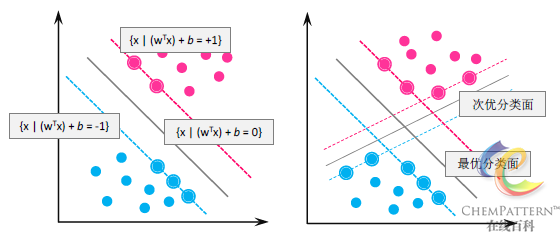
y_i{}({w^T}{x_i} + b) \geqslant 1,i = 1,...,n

因此同时满足上述两个条件的分类面即为最优分类面（图12-39），这两类样本中参与定义（使上式等号成立）最优分类面的样本即称为支持向量。

3）最优化问题

首先，根据上述推导所获得的目标函数和约束条件：

\max \frac{1}{{\left\| w \right\|}}s.t.,y_i{}({w^T}{x_i} + b) \geqslant 1,i = 1,...,n

可使求最优分类面的问题等价于求解一个标准的凸二次规划（quadratic programming，QP）问题，即：

\min \frac{1}{2}{\left\| w \right\|^2}s.t.,y_i{}({w^T}{x_i} + b) \geqslant 1,i = 1,...,n

凸二次规划的求解过程通常效率不高，但可通过拉格朗日变换为对偶变量的优化求解问题，从而提高算法的效率，但更重要的是为后面引入核函数做准备。定义如下目标函数：

\mathop {\max }\limits_{{a_i} \geqslant 0} L(w,b,\alpha ) = \mathop {\max }\limits_{{a_i} \geqslant 0} \frac{1}{2}{\left\| w \right\|^2} - \sum\limits_{i = 1}^n {{\alpha _i}{\color{Blue}[{y_i} \cdot ({w^T}{x_i} + b) - 1]}}

其中α_i为拉格朗日系数。注意到对于作为支持向量的x_i而言，上式中的蓝色部分将为0，非支持向量则不为0，而为了满足最大化，这些非支持向量的α_i则必须为零。因此再次从优化过程而非上文的几何直观中推导获得了支持向量的概念。

接下来，分为两步求解对偶学习问题，首先通过对w，b求偏导数并令其等0，使得L(w,b,a)关于w和b最小化：然后求对α的函数最大值。

\begin{gathered} \mathop {\max }\limits_a \sum\limits_{i = 1}^n {{a_i} - \frac{1}{2}} \sum\limits_{i,j = 1}^n {{a_i}{a_j}{y_i}{y_j}x_i^T{x_j}} \hfill \\ s.t.,{a_i} \geqslant 0,i = 1, \ldots ,n = 0,\sum\limits_{i = 1}^n {{a_i}{y_i} = 0} \hfill \\ \end{gathered}

4）SMO算法

上述求解凸二次规划问题的一个更加高效的重要优化算法SMO（sequential minimal optimization）由John C. Platt在1998年提出。其核心思想是通过将原问题分解为一系列小规模凸二次规划问题从而获得原问题的解。具体过程在此不再赘述。ChemPattern采用了SMO算法进行凸二次规划问题的求解。

5）最优分类函数

根据KKT（Karush-Kuhn-Tucker）定理求解上述问题，最终获得最优分类决策函数：

f(x) = \operatorname{sgn} \left( {\sum\limits_{i = 1}^n {a_i^*{y_i}\left\langle {{x_i},x} \right\rangle + {b^*}} } \right)

其中sgn( )为符号函数，即根据输出结果的正负号进行类别的预测。x_i为支持向量，x为待测向量。a_i^*，b_i^*表示求取的最优解，b作为分类的阈值可由任意一个支持向量求取。

在该公式中：1）对于测试集样本x的预测，只需计算其与训练集的向量内积\left\langle {{x_i},x} \right\rangle 即可，这为支持向量机的高维非线性推广提供了前提条件；2）只有支持向量的a_i^* > 0，因此前述的内积计算只需针对少量的支持向量而不是整个训练集数据，故识别时的计算复杂程度只取决与支持向量的个数。

6）核函数

上述讨论的均为线性可分简单的情况，而实际应用中的复杂体系样本在原始空间中常常是线性不可分的，因此引入了数据升维的概念，从而将数据从低维输入空间通过非线性映射函数\varphi (x)映射到高维特征空间，在这个空间中尝试构造最优分类超平面。可以证明，如果选用恰当的映射函数\varphi (x)，输入空间线性不可分问题在特征空间将转化为线性可分问题（图12-40）。

此时的最优分类函数以\varphi ({x_i})与\varphi (x)的内积形式可表示为：

f(x) = \operatorname{sgn} \left( {\sum\limits_{i = 1}^n {a_i^*{y_i}\left\langle {\varphi ({x_i}),\varphi (x)} \right\rangle + {b^*}} } \right)

为了克服直接在高维空间中进行内积运算时带来的“维数灾难”（12.23）等诸多问题，采用与之等价的积分核函数（kernel function）来计算样本向量在低维空间中隐式映射过后的内积，从而为高维特征空间解决复杂体系分类问题奠定了理论基础。

左图：输入空间；中图：特征空间非线性映射， \dpi{90}\Phi :{\mathbb{R}^2} \to {\mathbb{R}^3},({x_1},{x_2}) \mapsto ({z_1},{z_2},{z_3}) = (x_1^2,\sqrt 2 {x_1}{x_2},x_2^2)

用核函数K({x_i},x)代替\left\langle {\varphi ({x_i}),\varphi (x)} \right\rangle ，则判别函数变为：

f(x) = \operatorname{sgn} \left( {\sum\limits_{i = 1}^n {a_i^*{y_i}K({x_i},x) + {b^*}} } \right)

采用核函数后，不需要知道非线性映射函数\varphi (x)的具体形式和参数。常用的核函数类型有：

线性内积函数K({x_i},x) = x_i^Tx
多项式内积函数K({x_i},x) = {\left[ {x_i^Tx + 1} \right]^q}
径向基内积函数K({x_i},x) = {e^{ - {{\left\| {{x_i} - x} \right\|}^2}/2{\sigma ^2}}}，亦称高斯核函数。通过调控参数σ ，高斯核具有相当高的灵活性（图12-41），因此也是使用最广泛的核函数之一。

采用左图的多项式核函数和右图的高斯（径向基）核函数计算如图所示分类样本集的最优分类面。可观察到采用高斯核的决策函数的最优分类面的构造更好，并且所需支持向量较少。

7）软间隔

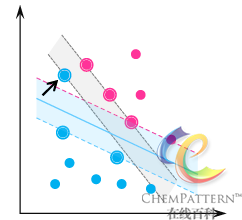
通过将原始数据映射到高维空间后，能够使两类样本线性分隔的概率大为增加，但当样本向量所包含系统误差（噪音）或为离群值时，高维下的超平面将仍无法使样本完全分开。因此引入松弛变量{\xi _i},{\xi _i} \geqslant 0,i = 1, \cdots ,n，即对应样本x_i相对于间隔位置的允许偏移量（软间隔）。使超平面的目标函数和约束条件相应修改为：

\begin{gathered} \min \frac{1}{2}{\left\| w \right\|^2} + C\sum\limits_{i = 1}^n {{\xi _i}} \hfill \\ s.t.,y_i^{}({w^T}{x_i} + b) \geqslant 1 - {\xi _i},i = 1,...,n \hfill \\ \end{gathered}

其中，C称为惩罚因子，起到控制对错分样本惩罚程度的作用，从而实现经验风险和置信风险之间的折中。经过上述修改后的最优分类超平面与其原始形式的唯一区别是α_i的约束条件变为0 \leqslant {a_i} \leqslant C。

采用软间隔方法排除箭头所示的离群值样本，从而获得校正后的最优分类超平面

8）多类支持向量机

支持向量机是一种典型的两类（二值）分类器，判别决策函数的输出值只有正、负判别信息。为了将基本算法推广到多类分类问题，先后提出了下列多类支持向量机算法：

通过某种方式构造一系列的两类分类器并将其组合在一起从而实现多类分类；
将多个分类面的参数求解合并到一个最优化问题中，通过求解该最优化问题一次性地实现多类分类。

其中第一类方法优点较多，更为常用，以下仅对第一类方法进行介绍。

一对其余SVMs（1-v-r SVMs，one-against-rest SVMs）
该方法依次构造一个两类分类器从而将每一类与其它所有类别区分开来。分类时将未知样本判为具有最大分类函数值的对应分类。该方法简便直观，但缺点是1）每个分类器中的两类样本集容量不平衡（倾斜）；2）每个分类器在训练时需要使用总训练集，效率相对偏低；3）可能存在样本得不到归属的不可分类情况。
一对一SVMs（1-v-1 SVMs，one-against-one SVMs）
该方法在每两类间训练一个分类器，因此对于一个多类问题，将有k(k-1)/2个分类器。对未知样本进行分类时采用“投票法”策略，即每个分类器都对其类别进行判断，也即“投票”，最后得票最多的类别即判为该未知样本的分类。该方法的缺点同样显而易见：1）可能存在两个以上分类的投票数相等的情况；2）对于较多类别的分类问题，需要构建k平方级数量的分类器，并且分类效率较低。
有向无环图SVMs（DAG-SVMs，directed acyclic graph SVMs）
在训练阶段和一对一SVMs投票一样，也需要构造出每两类间的分类函数，即有k(k-1)/2个分类器。但是在分类阶段，该方法构造一种两向有向无环图。当对未知样本进行分类时，首先从顶部的根节点开始，根据根节点的分类结果用下一层中的左节点或者右节点继续分类，直到达到底层某个叶为止，该叶所表示的类别即未知样本的类别。由此可见分类效率将比一对一SVMs有较大改善。

采用软间隔方法排除箭头所示的离群值样本，从而获得校正后的最优分类超平面

至此，一个可以处理线性和非线性的多个分类样本，并能妥善处理噪音和离群值的支持向量机才得以完整地实现。

支持向量机的特点

支持向量机在原理上的独特之处使其相对它模式识别方法而言具有一些突出特点：

传统的统计方法只有在样本数趋向无穷大时其性能才有理论上的保证。对于应用中的有限样本难以取得理想的效果。支持向量机是一种有坚实理论基础的新颖的小样本学习方法，基本上不涉及概率统计问题，因此本质上它避开了从归纳到演绎的传统过程，实现了高效的从训练样本到预报样本的“转导推理”。
传统的多元统计方法假设实际问题中总存在较少数目的一些“强特征”，用它们的简单函数（如线性组合）就能较好地逼近未知的函数。因此，需要仔细地选择提取一个低维的特征空间，在这个空间中用常规的统计技术来求解一个逼近。
而支持向量机所秉承的研究思路则认为实际问题中存在较大数目的一些“弱特征”，它们“巧妙的”的线性组合可较好地逼近未知的依赖关系。因此，采用什么样的“弱特征”相对并不重要，更重要的是如何形成“巧妙的”线性组合。
现实世界复杂的应用需要有比线性函数更富有表达能力的假设空间，因此解决样本空间中的高度非线性问题是支持向量机的核心价值所在。通过将样本“升维”，即非线性映射到高维甚至无穷维空间，再在高维特征空间中进行线性问题处理的思路圆满地解决了该难题。其中的核方法用于定义隐式的特征空间，使得非线性扩展后的计算复杂程度没有增加，这成为有效运用高维特征空间的关键所在。
支持向量机的最终决策函数只由少数的支持向量所确定，计算的复杂性仅取决于支持向量的数目，而不是样本空间的维数，从而在某种意义上避免了“维数灾难”。与人工神经网络相比，支持向量机方法本质上是对支持向量样本的加权。当自变量与因变量间蕴涵的复杂非线性关系尚不明了时，基于关键样本的方法可能优于基于因子的加权。同时，仅保留少量的支持向量不但可以剔除大量冗余样本，而且注定了该方法的简便性和健壮性。
由于有较为严格的统计学习理论做保证，应用支持向量机方法建立的模型具有较好的推广能力。支持向量机可以给出所建模型的推广能力的确定的界，这是目前其它任何学习方法所不具备的。此外，建立支持向量机模型所需要的先验人为干预较少，因此相对更客观。

核函数的选取和参数优化

支持向量机的精度受核函数种类及参数的影响较大，如高斯核的宽度，多项式核的阶数等。如何针对不同的应用问题选择恰当的核函数及其参数，以及松弛变量和惩罚因子的选取，尚无通行的规则。目前通过网格搜索（grid search）结合交叉验证方法来递归检索合适的模型参数配比是一种较为有效的方法。