相关系数(Correlation coefficient),是皮尔逊积差相关系数(Pearson product-moment correction coefficient)的简称,用于度量两组变量X和Y之间的线性密切程度的无量纲指标,以对相关和回归理论贡献较大的英国数理统计学家卡尔•皮尔逊的名字命名。相关系数系可根据方差及协方差矩阵计算获得。
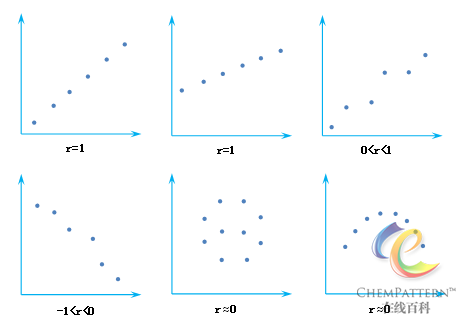
{r_{xy}} = \frac{{\operatorname{cov} (x,y)}}{{{S_x}{S_y}}} = \frac{{\operatorname{cov} (x,y)}}{{\sqrt {\operatorname{cov} (x,x)\operatorname{cov} (y,y)} }} = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} {\text{ }}\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} } }}相关系数的可能取值如下(图12-6):
相关系数相似度的一个重要的数学特性是,两组变量的位置和尺度的变化并不会引起系数的改变(如图12-6中所示),因此:

使用相关系数相似度时应注意以下几点:
| 自变量个数 n | 自由度 ν | 概率P (双侧) | |
|---|---|---|---|
| 0.05 | 0.01 | ||
| 3 | 1 | 0.997 | 1.000 |
| 4 | 2 | 0.950 | 0.990 |
| 5 | 3 | 0.878 | 0.959 |
| 6 | 4 | 0.811 | 0.917 |
| 7 | 5 | 0.755 | 0.875 |
| 8 | 6 | 0.707 | 0.834 |
| 9 | 7 | 0.666 | 0.798 |
| 10 | 8 | 0.632 | 0.765 |