12.14 多元线性回归

多元线性回归（multiple linear regression，MLR）用于分析一个因变量与多个自变量之间的线性关系，是最经典的回归分析方法。多元线性回归的处理方法与一元线性回归基本一致。许多非线性回归（non-linear regression）和多项式回归（polynomial regression）问题也都可通过转化为多元线性回归来解决。

A）多元线性回归模型

上式为多元线性回归模型的一般形式，其中，{\beta _0}为常数项，又称截距，{\beta _1},{\beta _2}, \cdots ,{\beta _m}称为偏回归系数。上式表示数据中因变量Y可以近似地表示为自变量{X_1},{X_2}, \cdots ,{X_m}的线性函数，而e则是去除m个自变量对Y影响后的随机误差，也称残差。

多元线性回归分析一般可分为两个步骤：

• 根据样品数据采用最小二乘法求得模型参数{\beta _1},{\beta _2}, \cdots ,{\beta _m}的估计值${b_0},{b_1},{b_2}, \cdots ,{b_m}$，从而得到表示因变量Y与自变量{X_1},{X_2}, \cdots ,{X_m}数量关系的表达式，即多元回归方程：
\hat Y = {b_0} + {b_1}{X_1} + {b_2}{X_2} + \cdots + {b_m}{X_m}

其中\hat Y表示Y的估计值

• 对回归模型质量进行评价（方程的拟合效果及预测效果）以及调整，对回归显著性进行假设检验，对各自变量进行假设检验，并对其作用大小做出评价。

B）回归方程的假设检验

为了确定所建立回归方程及其引入的自变量是否具有统计学意义，需要开展假设检验。通常采用的方差分析法可以将回归方程中所有自变量{X_1},{X_2}, \cdots ,{X_m}作为一个整体来检验其与因变量Y之间是否具有显著的线性关系。

如果P<α，则在α水平上拒绝H₀，接受H₁，认为因变量Y与m个自变量{X_1},{X_2}, \cdots ,{X_m}之间存在线性回归关系。

C）决定系数R²

根据方差分析的结果，还可以获得多元线性回归的决定系数R²。

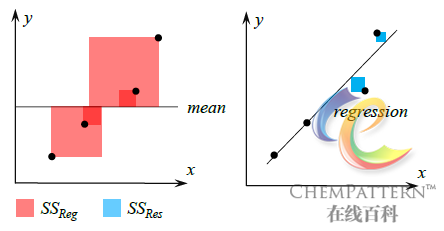
其中0≤R²≤1，说明自变量{X_1},{X_2}, \cdots ,{X_m}能够解释Y变化的百分比。该值越接近1，则说明模型对数据的拟合程度越好（图12-12）。当数据间不具备任何线性关系的情况下，该值可能取到负数。

D）复相关系数

R = \sqrt {{R^2}}称为复相关系数，可用来度量因变量Y与多个自变量X间的线性相关程度，亦即观测值Y与估计值\hat Y之间的相关程度。当为单自变量时，R = \left| r \right|，即简单相关系数。

E）校正决定系数

决定系数R²可用于评价回归模型的优劣，但R²具有随自变量数目增加而增大的趋势，因此不能直接用于两个具有不同个数自变量的回归模型的比较。此时可采用校正决定系数，表示为R_{adj}^2或\bar R{ & ^2}。

F）各自变量的假设检验与评价

进一步地，为了对每一个自变量的作用进行检验并评价其对于因变量Y的影响大小，可对每个自变量X_j分别进行t检验，并根据计算获得的显著性P_j值判断对应的X_j是否与Y具有线性回归关系。此外，可按t值从大到小的顺序排列各自变量，即为自变量对Y回归所起作用的重要程度排序结果。

G）残差分析

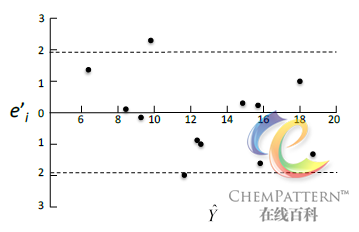
残差分析（residual analysis）是检验各个观测样本是否符合模型条件的重要方法之一。如果样本与模型的假设偏离较大，则作为离群值可能对建模造成不利影响。残差是指观测值Y_i与估计值\hat Y_i之差，即e=Y_i - \hat Y_i。残差分析具有以下特点：

• 正常情况下残差应服从均数为0，方差为{\delta ^2}的正态分布。
• 若\hat e_i呈一定的曲线变化，则表明因变量Y与自变量X间的关系可能为非线性，或者残差\hat e_i不独立，可考虑对自变量X进行变换后再进行线性回归分析；
• 若残差的分布不是较均匀地分布于均值0的直线上下两侧，而是随\hat Y_i的增加而扩散或收敛，则说明方差齐性（homoscedasticity, homogeneity of variance）的假设不能成立，可考虑对自变量X进行校正。

• 标准化残差\hat e_i近似服从均数为0，方差为1的标准正态分布。超过正态分布±1.96σ（P=0.05）的样品表明其回归拟合值的偏差具有显著意义，属于离群值。但如果该离群值确定并非由观测误差引起，则不应轻易剔除，以免损失重要信息。

H）杠杆值

杠杆值（leverage）用于衡量样本对于回归的影响程度大小。通常远离样本中心的观测点具有较大的杠杆值。

I）逐步回归法

在复杂体系的研究中，由于可能大量包含未知组分，因此回归模型所包含的自变量难以预先确定，如果将一些不重要的自变量引入方程，将会降低模型的精度。因此有必要尽可能只选择有意义的自变量用于建立回归方程，而将回归效果不够显著的自变量加以排除。该类优选方法有很多，此处仅对应用最广泛的基于逐步选择法的逐步回归法进行详细介绍。

该方法将自变量从无到有，由少到多地逐个引入回归方程中，从而获得“最优”回归方程。规则为设定一对F检验的入选检验水平aIn和剔除检验水平a_Out，并且a_Out≥a_In。

• 第1步，针对每一个自变量X分别对因变量Y做直线回归，并通过F检验，将具有统计学意义（a<a_In）的并且是最大F值的自变量X引入回归方程中；
• 第2步，考察再加入另一个剩余自变量时的各个回归方程，选择a<a_In并且是最大F值的自变量引入回归方程中；
• 第3步，按先剔除后选入的原则，考察当前回归方程中是否有需要剔除的变量，即a>a_Out；
• 第4步，重复第2步至第3步，直至既不能剔除也不能引入自变量，则逐步回归分析结束。

入选和剔除标准的选择有时对逐步回归分析的“优化”结果影响较大，因此对于逐步回归所得到的结果不能不加分析地盲从，而必须同时结合问题本身和专业知识来判断。

J）多重共线性

多重共线性是指部分自变量之间存在较强的线性关系，这种情况在复杂体系分析中极为常见。如果这种相关程度非常高，则使用最小二乘建立的回归方程可能不稳定（病态）或失效（与客观实际不符）。消除多重共线性的方法有很多，譬如采用逐步回归或改用偏最小二乘回归等。

K）方程维度限制

进行元线性回归通常要求样本个数n为自变量个数m的数倍（譬如n=5m~10m），否则建立的回归方程将不够稳定。当样本个数小于自变量个数时，回归方程将无法计算。而对于复杂体系分析而言，仪器所采集的样本数据的自变量数目通常较大，此时可考虑采用偏最小二乘回归或先进行数据降维。

L）模型评价

模型（质量）评价主要对所建立的回归模型的预测能力进行评价，以尽量避免模型过拟合（over-fitting）现象的发生。其中交叉验证（cross validation）是最常用的模型验证方法，该方法通过将数据集依次随机划分为校正集和验证集从而进行模型的评价。详见12.20交叉验证方法。但由于多元线性回归本身并不具备区分原始数据矩阵中所存在的噪音的能力，因此相对容易导致过拟合的情况发生，此时可考虑采用偏最小二乘回归代替。

M）回归估计与预测

建立回归模型的出发点和主要目的之一在于对因变量Y未知的待测样品进行回归预测。预测结果\hat Y_i通常包含两类误差，一是回归模型只能解释样本数据的部分方差来源，而不能（也不应）完全精确地描述样本数据；二是采样误差，即回归建模所使用的样本并不能完全代表样本集的实际分布，因此距离数据均值越远的预测值，其置信区间范围也越宽，提示有预测误差增大的趋势（图12-14）。