12.16 典型相关分析和多元方差分析

典型相关分析

典型相关分析（canonical correlation analysis，CCA）是线性回归用于多个因变量分析时的推广形式，由美国统计学家Harold Hotelling于1936年提出。该方法寻找一组自变量的线性组合和一组因变量的线性组合，称为第1对典型相关变量或简称典型变量（canonical variate），并使其之间的相关性最大化，接下来与第1组正交且相关性次大化的变量线性组合称为第2对典型变量，依次类推。

在实际应用中，典型相关分析具有以下特点：

上图显示3个样本分组的MANOVA分析通过2个自变量的线性组合从而获得更好的组间分离，从而在该问题上优于PCA的自变量降维效果

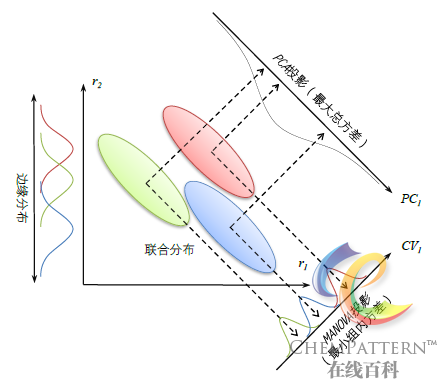
• 典型相关分析发展了主成分分析（12.14）的思想，并进一步同时考虑因变量的线性组合及其与自变量间的相关性，而不像主成分分析一样仅获得自变量的线性降维（图12-20）。它也构成了多元方差分析（multiple analysis of variance, MANOVA）以及多元判别分析（multiple discriminant analysis）的核心部分，即寻找使得组间分隔最大化的自变量的线性组合。但在回归分析方面，目前通常可由性能更为优异的偏最小二乘回归（12.17）所替代。

回归模型	自变量X 个数	因变量Y 个数	相关性评价
一元线性回归	1	1	简单相关系数
多元线性回归	m (m≤n)	1	复相关系数
典型相关分析	m (m≤n)	p	典型相关系数
偏最小二乘回归	m	p	决定系数

• 与主成分分析类似，典型相关分析的最终结果包括典型变量载荷（canonical loadings）和典型变量（得分）等，可用于对结果进行专业解读。
• 与主成分分析类似，典型相关分析对于数据中的偶然相关性（capitalization on chance）高度敏感，可能导致模型的过拟合，因此必须对其结果的有效性进行充分的验证（如交叉验证），而不能不加判别地使用。
• 与主成分分析中的主成分保留数目原则不同，典型相关分析中保留过多的典型变量通常不仅没有显著的统计学意义，而且从专业知识角度也难于解释，因此通常只取第1个或前2个典型相关变量做解释即可。

数学部分

• 根据样本集的两组变量X和Y，找出两组线性组合{u_1}{\text{ = }}X{b_1}与{t_1} = Y{a_1}中的a₁, b₁值，使得相关系数r({t_1},{u_1})最大化，其中， r({t_1},{u_1}) = \frac{{\operatorname{cov} (t,u)}}{{\sqrt {\operatorname{var} (t)\operatorname{var} (u)} }}, \operatorname{cov} (t,u) = a'{R_{YX}}b
• 对t和u进行数据标准化（标度化），使得问题求解转化为当a'{R_{YX}}a = 1和b'{R_{YX}}b = 1时的a'{R_{YX}}b最大值这一约束最大化问题，并最终通过特征值分解求出a₁, b₁值；
• 重复第1步，找出第2组a₂, b₂值，并保证r({t_1},{t_2}{\text{) = 0}}和r({u_1},{u_2}{\text{) = 0}}，依次类推。

多元方差分析

正如典型相关分析是线性回归的多变量拓展一样，与之有着密切联系的多元方差分析则是方差分析的多变量推广形式。多元方差分析的步骤通常如下：

• 做多个因变量的多个均数假设检验，假定g（g≥2）组样本观测值分别来自正态总体N({\mu _1},{\sigma ^2}),N({\mu _2},{\sigma ^2}), \cdots ,N({\mu _m},{\sigma ^2})，根据样本均数向量{\bar X_1},{\bar X_2}, \cdots ,{\bar X_g}推论{H_0}:{\mu _1} = {\mu _2} \cdots = {\mu _g}是否成立。
• 如同在多元线性回归分析中采用F检验来考察回归模型的显著性一样，在典型相关分析中，采用相似的Wilks’ Λ（称为Wilks’s Lambda）统计量来对计算获得的典型变量开展上述假设检验。
• 接下来，可在假设H₀不成立的结论基础上，采用基于Wilks’ Λ的Bartlett’s 卡方检验（详见12.15主成分分析与奇异值分解）依次进行一系列部分分组间的均值不等的假设检验，即确定有具体有几个分组之间的均值不相等，以进一步考察各分组均值所在的空间维度。 V = - \left[ {(n - 1) - \frac{{p + q + 1}}{2}} \right]\ln \Lambda

  其中，n为样本观测数，p为自变量X数目（即矩阵X的秩），q为因变量Y数目（即矩阵Y的秩），V为具有（p，q）自由度的近似{\chi ^2}分布。

• 最后，还可根据典型相关分析的结果，绘制出各分组的样本在典型变量（CV）空间的投影（得分）散点图及载荷图。并可依据各分组均值间的马氏距离绘制出各分组的系统聚类图。