簇类独立软模式法(soft independent modeling of class analogies,亦作standard isolinear method of class assignment,SIMCA)由瑞典统计学家Herman Wold于1976年提出,是一种基于主成分分析(12.15)的有监督模式识别方法。该方法解决了主成分分析在建模时不包含分类信息,因而不能直接用于模式识别的问题。其核心思想是对训练集中的每个样本分类分别建立一个主成分分析模型以对其进行描述,并在此基础上,通过将未知样本依次拟合各分类的主成分模型,从而预测该未知样本的分类。
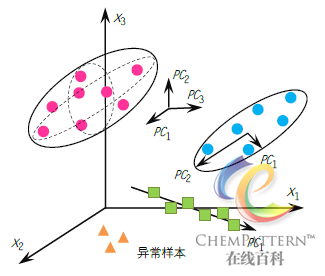
一个SIMCA模型包含了训练集中各个分类的PCA子模型。每个PCA 分类子模型的最佳主成分数可通过交叉验证技术以预测残差平方和(PRESS,prediction error sum of squares)进行判断。由于每个独立的模型可以选取不同的主成分数,因此不同模型在输入空间中可能表现为线、平面或超平面等各种形状(图12-44)。

首先对训练集中的各类分别建立各自的PCA模型:
\begin{gathered} X = T{P^T} \hfill \\ {x_j} = {x_C} + \sum\limits_{i = 1}^k {{t_i}p_i^T} + e = {x_C} + {t_1}p_1^T + {t_2}p_2^T + \cdots + {t_i}p_i^T + e \hfill \\ \end{gathered}式中,t为得分向量,p为载荷向量,xc为模型的均值向量。模型的主成分保留数为k,剩余的方差合并入残差矩阵E。
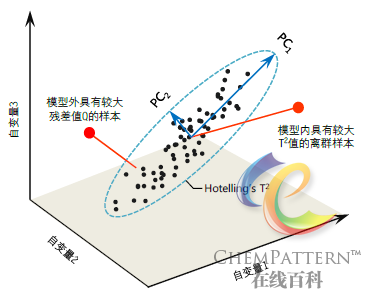
接下来,引入以下两个统计量来综合衡量样本与PCA模型的拟合程度,从而在主成分特征投影超平面中定义封闭的分类判定边界。
1)模型拟合残差Q
残差Q为样本与PCA模型中k个主成分上投影之间的残差,即样本中不被模型所解释的部分,用于评价样本与给定的模型拟合程度的好坏,如下式:
{Q_i} = {e_i}e_i^T = {x_i}(I - {P_k}P_k^T)x_i^T其中ei样品i的残差向量,Pk为保留k个主成分的PCA模型的载荷矩阵,I为自变量数目的单位矩阵。
2)Hotelling's T2
Hotelling's T2统计量用于描述样本在PCA模型内部的远离程度,即主成分投影超平面上距中点的距离,其定义如下:
{\text{T}}_i^2 = {t_i}{\lambda ^{ - 1}}t_i^T = {x_i}{P_k}{\lambda ^{ - 1}}P_k^Tx_i^T其中ti为样本i的得分向量,λ为特征值的对角矩阵(λ1到λk)。T2和马氏距离(12.7)此处是等价的。
进而根据该PCA模型中所有训练集样本的残差Q和T2统计量的分布估计,分别求出对应的置信限。这里给出对T2统计量置信限的计算公式如下:
T_{m,k,\alpha }^2 = \frac{{k(m - 1)}}{{m - k}}{F_{k,m - k,\alpha }}式中m为样本数,k为主成分数,F代表显著性为α的F检验。
依次将待测样本与每个PCA模型进行拟合(投影),进而计算残差Q和T2统计量,当满足给定判据时,即认为该未知样本属于模型所代表的分类类别。
\begin{gathered} {d_{ij}} = \sqrt {{{({Q_r})}^2} + {{(T_r^2)}^2}} \hfill \\ {x_{test}} \in {\omega _j},{\text{ }}if{\text{ }}{d_{ij}} < \sqrt 2 \hfill \\ \end{gathered}其中dij为样本i距离模型j的Q与T2加权距离,Qr和Tr2分别为Q、T2与显著性α下的对应概率分布置信限的比值。
除此之外,也可采用拟合残差的F统计量的单边临界值{F_0} = [\alpha ,(n - k),(m - k)](置信水平σ通常取0.01或0.05,m为第p类的样本数,n为自变量数,k为保留主成分数),以及主成分得分的±0.5S标准差等两个判定边界作为该模型的分类依据。
SIMCA方法是主成分分析方法在模式识别领域的拓展,其具有以下显著特点: