12.17 偏最小二乘回归

偏最小二乘回归方法（partial least squares regression，PLS）由瑞典统计学家Herman Wold于1975年提出。该方法是化学计量学多元校正技术的代表，在化学计量学特别是近红外光谱多元校正分析中得到了广泛的应用，已成为一种标准的多元建模工具。

偏最小二乘回归是对多元线性回归模型的拓展。其最简形式为一个描述因变量Y和自变量X之间关系的线性模型：

Y = {\beta _0} + {\beta _1}{X_1} + {\beta _2}{X_2} + \cdots + {\beta _p}{X_p}

其中β0为截距，βi为自变量Xi的回归系数。PLS的基本模型为：

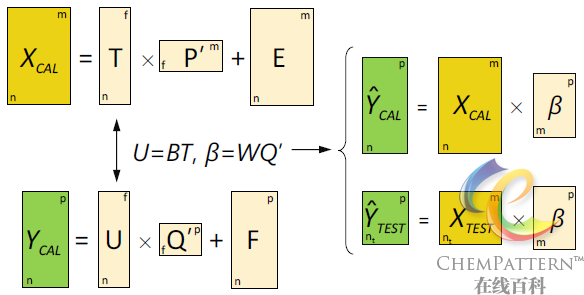
\begin{gathered} X = T{P^T} + E \hfill \\ Y = U{Q^T} + F, \hfill \\ \end{gathered}

其中X（n×m）为自变量矩阵，Y（n×p）为因变量矩阵；T和U（n×f）分别为X的潜变量（Latent variable，LVs，亦称主因子）得分矩阵（X的投影）以及Y的潜变量得分矩阵（Y的投影）；P（m×f）和Q（p×f）分别为正交的载荷矩阵；E和F分别为拟合残差矩阵。其中X和Y以确保T和U协方差最大化的原则进行分解（图12-21）。

图12-21 偏最小二乘回归的矩阵分解

PLS的算法包括非线性迭代偏最小二乘算法（Nonlinear Iterative Partial Least Squares，NIPALS）以及快速算法SIMPLS 。其计算过程如下式所示：

\begin{gathered} {w_\alpha } = {X^T}y \hfill \\ {t_\alpha } = X{w_\alpha } \hfill \\ {q_\alpha } = {y^T}{t_\alpha } \hfill \\ {p_\alpha } = {X^T}{t_\alpha } \hfill \\ \beta = W{({P^T}W)^{ - 1}}q \hfill \\ \end{gathered}

其中α为潜变量（LVs）数， w，t，p，β分别为权重、得分、载荷和回归系数矢量。

A）偏最小二乘回归与传统多元统计方法的区别

在经典的多元线性回归模型和以其为基础的多元统计方法如判别分析、典型相关分析和主成分回归中，变量X和Y的因子分别从X'X和Y'Y的协方差矩阵中提取，无法同时表示X和Y的相关性，而偏最小二乘回归的预测方程由自Y'XX'Y 协方差矩阵中提取获得的因子来描述。此外偏最小二乘回归可能是所有多元校正方法里对变量约束最少的方法，这种灵活性使它适用于传统的多元校正方法受到制约的许多场合，如当样本观测数小于自变量数时。

在偏最小二乘的算法中，可以同时实现回归建模（多元线性回归）、数据降维（主成分分析）以及两组变量之间的相关性分析（典型相关分析）。这是多元统计数据分析中的一个飞跃，偏最小二乘法也因此被称为第二代回归方法。

综上所述，与传统多元线性回归模型相比，偏最小二乘回归具有以下特点：

  • 偏最小二乘法≈多元线性回归分析+主成分分析+典型相关分析；
  • 能够在自变量存在严重多重共线性的条件下进行稳健的回归建模；
  • 允许在样本数少于变量数的条件下进行回归建模；
  • 偏最小二乘回归在最终模型中将包含原有的所有自变量；
  • 偏最小二乘回归模型更易于辨识系统信息与噪声；
  • 在偏最小二乘回归模型中，每一个自变量的回归系数更容易解释。

    • B）偏最小二乘回归模型的质量评价

    对偏最小二乘回归模型的质量评价分为建模能力和预测能力等两方面，在化学计量学中常用的参数包括模型解释率R2X、R2Y，以及预测误差PRESS（Prediction error sum of squares）和预测率Q2X、Q2X，这些评价指标都属于均方误差（Mean squared error，MSE）的范畴。其中对预测性能的估算需要采用交叉验证的方法（详见12.20交叉验证方法）。

    \dpi{100} \begin{gathered} {R^2}X = 1 - \sum {{{\left( {\hat X - X} \right)}^2}/\sum {{X^2}} } \hfill \\ {R^2}Y = 1 - \sum {{{\left( {\hat Y - Y} \right)}^2}/\sum {{Y^2}} } \hfill \\ {Q^2}X = 1 - \sum {{{\left( {{{\hat X}_{PRED}} - X} \right)}^2}/\sum {{X^2}} } \hfill \\ {Q^2}Y = 1 - \sum {{{\left( {{{\hat Y}_{PRED}} - Y} \right)}^2}/\sum {{Y^2}} } \hfill \\ PRESS = \sum {{{\left( {{{\hat Y}_{PRED}} - Y} \right)}^2}} \hfill \\ \end{gathered}

    通常地，Q2Y开始时会随着所保留的潜变量个数的增加而提高，但达到一定程度后，Q2Y将不再增大甚至减小，说明此时的模型已经发生过拟合。因此模型的潜变量保留个数应以Q2Y最大值处为准。

    C）回归方程的假设检验及评价

    与主成分分析一样，对于给定的任何数据，偏最小二乘回归总能够给出明确的解，而无论原始数据的X、Y矩阵之间是否真正存在非偶然的线性相关关系。对偏最小二乘回归方程的假设检验可参考12.14多元线性回归。

    D）偏最小二乘判别分析（PLS discriminant analysis, PLS-DA）

    偏最小二乘判别分析是偏最小二乘回归的特殊形式，其采用二值化的Y矩阵进行回归建模。偏最小二乘判别主要用于模式识别，此外也可以作为数据降维方法用于和主成分分析类似的用途。